Two basic strategies for 9/6 Triple Triple Bonus

Triple Triple Bonus Poker is a pretty rare game apparently. It also has a rare paytable entry: Four 2s to 4s with an ace kicker, which pays the same as the royal flush.

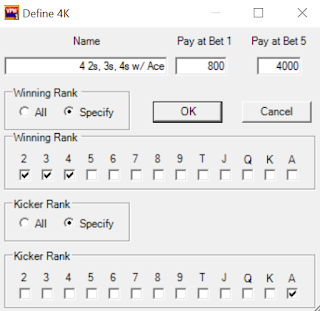
The Wizard of Odds Strategy Calculator (WOOSC) doesn’t support it, and neither does Video Poker for Winners (VPW) out of the box. But it’s possible to add a customized paytable for it in VPW. You need to go deep into the belly of the software, add a customized four-of-a-kind: with 2s-4s as the Winning Rank and an ace as the Kicker Rank:

For the 9/6 game, VPW then generates a strategy that it claims returns 99.73972%, with a claimed strategy error of 0.011847%.

Those numbers are just wrong. One can go look into VPW’s strategy report, to find the total error it claims in coins is ~1539.5, which makes the strategy’s error five times that number, 0.059237%. (I've already written about the bug in VPW that results in it miscalculating its strategies’ returns for customized games by a factor of five.)

But even that number is not correct. My software calculates VPW’s strategy error to be 0.015658%–0.141404%, depending on what the player chooses to hold when dealt ambiguous hands. On top of that, the strategy is not very comprehensible. For example, its 23rd option to hold is just "Low Pair Kicker" with no explanation or example. What is that supposed to mean? (I assumed the best, and in my calculations assumed it means 22A, 33A, or 44A. But it could also mean options such as 223 or 443. Who knows what an unsuspecting player may assume it means.)

Why does VPW’s strategy have such a relatively large error? What is it missing? So many things. It’s death by a thousand cuts: It has a line saying “THREE of a KIND 2-4,A with 2-4,A” which doesn’t help in figuring out which option to hold if dealt 4443A (4443 vs 444A). It prefers KHT to KK, QQ, JJ, while it’s better to hold the high pair. It recommends holding AHHT, while you get a higher average return if you just hold the ace. It prefers all SF3s with no high cards and one inside (SF3 0hi 1i) to an ace, while it’s usually better to hold the ace. It prefers JT to KH, while it’s generally better to hold KH, etc., etc.

Either way, VPW’s error is clearly too much for a basic strategy. Unless Triple Triple Bonus has a really weird straetgy, I felt I could do much better. Let’s see!

My strategy evaluation and generation software already supported Triple Double Bonus. It needed some slight modifications to support Triple Triple Bonus. After I added Triple Triple Bonus, I confirmed the software’s correctness by checking the return of the various paytables for the game against the information I could find about the game on the Wizard of Odds and vpFREE2. They matched, so I’m confident I’ve implemented the game correctly.

I started by trying to analyze the 9/6 paytable the normal way my software handles games, by looking at all different hand options (the same way WOOSC does). But that led to a hairy problem. I ran into thirty options that participate in loops together: some 4-card flushes with three high cards, some 3-card royal flushes, and some high pairs.

For example, in this game, ignoring penalty cards and averaging the different hands, AKJ2 is better to hold than AKJ, AKJ is better to hold than JJ, and JJ is better to hold than AKJ2. I know how to handle such situations, except there are twenty-seven other options also interacting in the same loopy way with these three options! I have written before on how a fifteen-long set of options needed more than a day of computation on a cloud server. A thirty-long set of options would require a hundred quadrillion years to find absolutely the best strategy. We definitely don’t have that much time.

(These groups of loopy options, where each option is better than another in a way that loops back to itself, are called a strongly connected component in graph theory, a field of discrete mathematics. My software finds such strongly connected components, tries to find the best order for them through brute force, and then inserts that solution among the other options, options that don't need such an approach for being put in order.)

So I needed to simplify and treat all 4-card flushes with three high cards as a single class of options. That change reduced the size of the thirty-option list to just seven. Now the best order among them could be computed in less than a second. This may have lowered the strategy’s return. How much lower, I have no clue. Anyway, the best order for these seven simplified options was calculated to be:
FL4 3h > RF3: AKQ, AKJ, AQJ > KK, QQ, JJ

With that out of the way, the rest was smooth sailing. The various 3-card straight flushes that are usually the source of problems didn’t cause any trouble this time (perhaps because the flush returns 6 times the bet?). Everything else was simple too.

So here is the strategy I found:

RF5; 4-OF-A-KIND-WITH-KICKER; SF5
4-OF-A-KIND; 3-of-a-kind-with-kicker: with ace
3-of-a-kind-with-kicker: without ace
AAA, 222-444 > FULL HOUSE > 3-OF-A-KIND: others
RF4 > FL5 > SF4 0i > ST5 > SF4 1i [incluces A-low]
AA > TWO PAIR
RF3: KQJ > FL4 3hi > RF3: AHH, QJT
KK, QQ, JJ
RF3: KHT > FL4: others > RF3: AHT
low pair with ace kicker: 22A, 33A, 44A
low pair: 22–44
KQJT
SF3: QJ9 > QJT9
88 > SF3: JT9 > 55–77, 99, TT
SF3: KQ9, KJ9, QJ8, 345–678
QJ; JT98
SF3: QT9, JT8, J98, 789, 89T
KH
ST4 0hi [2345–789T]
AKQJ
FL3 2hi
AH
SF3 1hi 2i [includes A-low]
SF3 0hi 1i: 234, 346
A
SF3 0hi 1i: others
KQJ9 > KQJ
KH, QJ
JT
FL3 1hi
KT, QT
K, Q, J
SF3 0hi 2i; FL3 0hi
five new cards

That's the best WOOSC-style basic strategy I could come up with. It returns 99.74831%, with an error of 0.003253%. It can be improved by either simplification (and thus losing some return), or by somebody smartly figuring out how that 30-option strongly connected component can be solved. But right now, it’s the best basic strategy I can come up with at such short notice.

If we decide to make the strategy simpler and avoid hard-to-remember seemingly random SF3 lists of options, we get to this strategy:

RF5; 4-OF-A-KIND-WITH-KICKER; SF5
4-OF-A-KIND; 3-of-a-kind-with-kicker: with ace
3-of-a-kind-with-kicker: without ace
AAA, 222-444 > FULL HOUSE > 3-OF-A-KIND: others
RF4 > FL5 > SF4 0i > ST5 > SF4 1i [includes A-low]
AA > TWO PAIR
RF3: KQJ > FL4 3hi > RF3: AHH, QJT
KK, QQ, JJ
RF3: KHT > FL4: others > RF3: AHT
low pair with ace kicker: 22A, 33A, 44A
low pair: 22–44
SF3 2hi 1i
KQJT, QJT9
88 > SF3 1h 0i > 55–77, 99, TT
SF3 2hi 2i
JT98
SF3 1hi 1i; SF3 0h 0i [excludes 234 and all A-low]
KH, QJ
ST4 0hi [2345–789T]
AKQJ
FL3 2hi
AH
SF3 1hi 2i [includes all A-low]
A
SF3 0hi 1i [includes 234]
KQJ9 > KQJ
KH, QJ
JT
FL3 1hi
KT, QT
K, Q, J
SF3 0hi 2i; FL3 0hi
five new cards

This VPW-style simpler strategy returns 99.74828%, with an error of 0.003291%. Just slightly worse than the WOOSC-style strategy.