Something wrong with Video Poker for Winners’ numbers?

I have been going through various strategies generated by Video Poker for Winners (VPW), and I believe I have found mistakes in both the strategies and the returns VPW reports.

This is a preliminary report. I don’t know how extended the problem is, but basically, while the strategies are good enough, there are obvious issues with some of them and some of their returns are incorrectly reported. For comparison, I looked at its free competitor for generating strategies, the Wizard of Odds Strategy Calculator (WOOSC). While not perfect (it doesn’t always generate the best basic strategy possible) and with strategies that are sometimes hard to decipher or remember, its numbers could be trusted for all the paytables I tried.

Some of the strategies in VPW appear to be curated for a specific paytable, so I went off the charts and tried unlisted games too. In this post, I report on Bonus Poker 6/5, which can be added as a “User Defined” paytable. (If you have the software, choose Bonus Poker 8/5 or 7/5, then choose “Options > Change Paytable” from the menu, then change the Full House's return to 6. Click “OK”, then name the game “Bonus Poker 6/5”. To see the strategy, select “Analyze > Strategy” from the menu.) According to the Las Vegas Advisor, this is the best game found in some Las Vegas bars, some of which have playable promotions.

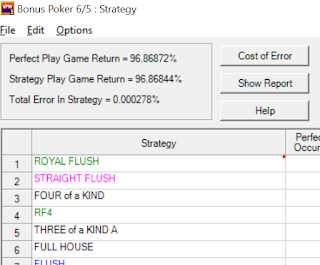
Bonus Poker 6/5 returns 96.86872%. VPW calculates that correctly. It generates a strategy for the game that it claims returns 96.86844%. It also claims its “Total Error in Strategy” is 0.000278%. One may compare those numbers with the WOOSC’s generated strategy, which reports a return of 96.8673% (with an error of 0.0014%) and assume that VPW’s strategy returns more. Unfortunately that's not true! In reality, WOOSC’s strategy returns slightly more.

For the record, here is the strategy I get from VPW version 1.81.0.0 (in case you get something different, please tell me in the comments):

1	ROYAL FLUSH
2	STRAIGHT FLUSH
3	FOUR of a KIND
4	RF4
5	THREE of a KIND A
6	FULL HOUSE
7	FLUSH
8	THREE of a KIND 2-K
9	STRAIGHT
10	SF4
11	TWO PAIR
12	HIGH PAIR J-A
13	RF3
14	FL4 2h; 1h; 0h
15	ST4 3h0i KQJT
16	Low Pair 2-4
17	ST4 2h0i QJT9
18	Low Pair 5-T
19	ST4 1h0i JT98
20	SF3 2h1i 'QJ9'; 1h0i 'JT9'
21	ST4 0h0i 2345-789T
22	SF3 2h2i 'QJ8'
23	ST4 4h1i AKQJ
24	SF3 2h2i 'KH9'
25	RF2 'QJ'
26	SF3 1h1i 'QT9'-'J98'; 0h0i '345'-'89T'
27	RF2 'AH'; 'KH'
28	ST4 3h1i AHHT-KQJ9
29	HC3 KQJ
30	HC2 QJ
31	SF3 1h2i 'KT9'-'J87'; A-low 'A23'-'A45'; 0h1i '234','235'-'79T'
32	HC2 KJ
33	RF2 'JT'
34	HC2 AH; KQ
35	HC1 A
36	RF2 'QT'
37	HC1 J-Q
38	RF2 'KT'
39	HC1 K
40	SF3 0h2i '236'-'69T'
41	Draw 5 new cards

First of all, there is clearly something wrong with the strategy. In its line #34, it says hold “AH; KQ”, while in this game KQ is always better than AK and AQ (and they all appear together in hands such as A♥K♦Q♣8♦7♠). So, the actual return of the VPW’s strategy for Bonus 6/5 depends on the player’s choice for hands that have unsuited AKQ, where both options AH and KQ appear in the same line #34.

At worst, if the player always chooses AH over KQ, the strategy returns 96.86268%, with an error of 0.006032% (note that AH comes before KQ in line #34, so this is a justifiable decision based on the provided strategy). At best, if the player always holds KQ, the strategy would return 96.86733%, with an error of 0.001388%. Both of these are far from the 0.000278% error VPW claims. The actual error is five to twenty-two times larger than claimed.

How can I prove my numbers? It’s not easy. They come out of a piece of software I’ve written. The software confirms the returns claimed by WOOSC to be accurate, but arrives at different numbers for the VPW strategy. I may provide the software publicly, but it won’t prove anything, since my software may have bugs too (proving software to be mathematically correct is an advanced field in computer science, and such proofs are very complicated).

But my claim can be verified in two ways.

One is through third parties, basically by other programmers independently trying to find the return of the VPW strategy and confirming either my numbers or VPW’s. The more people independently confirm my numbers, the higher the chance my numbers are correct. The more people independently confirm VPW’s, the higher the chance my numbers are incorrect.

Another way I can get to a proof, is by providing the list of hands the VPW strategy gets wrong and listing how wrong the strategy is for each hand. I have created a page on my website that lists all such hands. (I have also colored red the hands that are held wrong due to the "AH; KQ" line. You can remove those lines, and you can see that even after their removal, the strategy does not return as much as it claims.) In order to confirm my number, you need to multiply each line’s error by the number of hands that are similar to that line, and add them all up (you should get to 156.7712, or 36.0874 if you eliminate the red lines). Divide by the number of different hands in video poker (2,598,960), and you should arrive at the strategy’s total error (0.006032%, or 0.001388% if you ignore the red hands). It’s tedious work (that can be simplified by using some software or spreadsheet), but it’s as close as I get to a proof.

You may ask what are the larger sources of error in VPW’s strategy. The #1 offender is of course the "AH; KQ" line, which should be split into two lines, "KQ" followed by "AH". The next easy to find offender is preferring QJ to ace-low SF3s. Ace-low SF3s are always better than QJ in this game. Then there are various SF3 groups that can be split into smaller sets and then the pieces could be moved around. Of course VPW’s strategy is a reasonable strategy: no basic strategy is perfect and sacrifices are frequently made for the sake of simplicity. What is problematic is claiming a return higher than the actual return.

On top of all this, I believe VPW’s number for Bonus Poker 6/5 is impossible to achieve with such a “basic” strategy. I tried my absolute best with the help of my software, and the best return possible with a basic strategy for Bonus Poker 6/5 in VPW or WOOSC format is 96.86738%, with an error of 0.001338% (you can find that basic strategy here). So VPW’s number is not just wrong, it’s impossible.

I only had time to check VPW’s Jacks or Better and Bonus Poker games. I may try this for more games in the future and report my findings. Here are the numbers for the strategies I checked:

Strtegy	Claimed return	Actual return	Claimed error	Actual error	Error ratio
Jacks or Better 9/6	99.54291%	99.54291%	0.000999%	0.000999%	1
Jacks or Better 9/5	98.44817%	98.44215–98.44817%	0.001633%	0.001633–0.007658%	1–5
Jacks or Better 8/6	98.39175%	98.39175%	0.000936%	0.000936%	1
Jacks or Better 8/5	97.29692%	97.29089–97.29692%	0.0011516%	0.001516–0.007540%	1–5
Jacks or Better 7/5	96.14675%	96.14491%	0.000460%	0.002298%	5
Jacks or Better 6/5	94.99570%	94.99395%	0.000437%	0.002185%	5
Bonus Poker 8/5	99.16429%	99.15965–99.16429%	0.001680%	0.001681–0.006324%	1–4
Bonus Poker 7/5	98.01318%	98.00853–98.01318%	0.001519%	0.001519–0.006162%	1–4
Bonus Poker 6/5	96.86844%	96.86268–96.86733%	0.000278%	0.001388–0.006032%	5–22

In the table above, the last column, error ratio, is how large the actual error is compared to the error claimed by VPW. For example, if the actual error was 0.1% while VPW claimed 0.02%, the error ratio would be 5. All error ratios are expected to be 1: if the VPW software didn’t have any bugs in computing its own strategies’ returns, all the error ratios would have been 1.

Of the nine strategies I checked, only the returns for two of them, Jacks or Better 9/6 and 8/6 were calculated correctly. All the other returns are incorrect one way or another. When a range starts from 1, as six of the entries do, the problem is usually due to a “AH; KQ” line, where the error reported by VPW is for the best case scenario (where a KQ is always held instead of an AH). The worst case scenario, where the player always holds AH, has the higher error ratio.

Interestingly, the error ratio appears to be lower for games for which VPW already has a predefined paytable. The error ratio is larger for games defined by the user.

As for the source of the bug, apart from the bad “AH; KQ” strategy lines, it appears to be a division error! VPW has a feature that creates a strategy report. If you look at it for 6/5 Bonus Poker, it reports the best case scenario’s number (with KQ always > AH) which is 36.0874 as “Error in Coins”. But then instead of dividing it by 2,598,960 to get to the real error, it seems to be dividing it by 5 × 2,598,960!

I personally plan to continue using VPW’s strategies, but I will be careful. I will verify the strategies and their returns with my own software before trusting VPW’s numbers. I will also watch for those weird “AH; KQ” lines in the strategies.